三角形边长公式(三角形边长公式小学)

#头条教育星师计划#三角形的三边关系定理：任意两边之和大于第三边，任意两边之差小于第三边。

应用:

1、判断所给三条线段能否组成三角形。

判断方法::当最短两边的和大于最长边时能组成三角形

例:下列长度的三条线段，能否组成三角形。

①4cm，9cm，5cm。

②15cm，8cm，8cm

③6cm，7cm，13cm

④三条线段的长度比为2:3:5

答案提示:最短两边的和大于最长边时能组成三角形，等于或小于最长边时不能。因此②能组成，其余不能组成。

2、求第三边的取值范围。

例1、长度分别为2，7，x的三条线段能组成三角形，则x的取值可以是( )

A.4 B.5 C.6 D.9

答案提示:根据三角形三边关系定理，因为7－2﹤x﹤7+2，即5﹤x﹤9，所以应选C。

3、求等腰三角形的边长或周长。

例1、若等腰三角形的周长为10cm，其中一边长为2cm，则该等腰三角形的底边长为( )

A.2cm B.4cm C.6cm D.8cm

答案提示:等腰三角形要分类讨论:

①当2cm为底边时，则腰长为(10－2)÷2=4

此时三角形三边为2cm，4cm，4cm，根据最短两边的和大于最长边，能组成三角形。

②当2cm为腰长时，底边长为10－2－2=6

此时三角形的三边长为2cm，2cm，6cm，

因为2+2﹤6，所以不能组成三角形，因此应选A。

例2、若实数m，n满足丨m－2丨+√n－4=0，且m，n恰好是等腰三角形的两条边的长，则该等腰三角形的周长是_____。

答案提示∵丨m－2丨≥0，√n－4≥0，

∴m－2=0，n－4=0，

∴m=2，n=4

当2为腰长时，三角形三边长为2，2，4，因为2+2=4，不能组成三角形。当2为底长时，三角形三边长为4，4，2，因为2+4﹥4，能组成三角形，此时三角形周长为10。

4、化简含绝对值的式子。

例:已知a，b，c为三角形的三边长，化简

丨b+c－a丨+丨b－c－a丨－丨a－b+c丨

解:∵a，b，c为三角形的三边长，

∴b+c－a﹥0，b－c－a<0，a－b+c﹥0

∴丨b+c－a丨+丨b－c－a丨－丨a－b+c丨

=(b+c－a)+[－(b－c－a)]－(a－b+c)

=b+c－a－b+c+a－a+b－c

=－a+b+c

5、证明线段的不等关系

例:已知如图点O为△ABC内部一点，求证AB+AC﹥OB+OC。

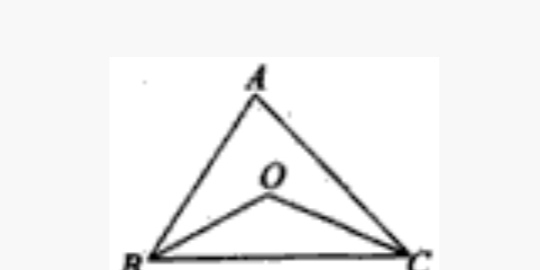
分析:因为要证明的四条线段间的关系不是同一个三角形的三边，可利用添加辅助线的方式把它们联系起来。

证明:延长BO交AC于点D

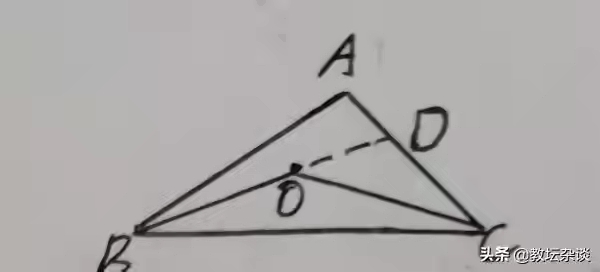
∵AB+AD﹥BD，BD=OB+OD

∴AB+AD﹥OB+OD

又∵OD+DC﹥OC

∴AB+AD+OD+DC﹥OB+OD+OC

又∵AD+DC=AC

∴AB+AC+OD﹥OB+OD+OC

∴AB+AC﹥OB+OC